
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I. Introduction
Dans ces vingt dernières années, le
développement des techniques satellitaires a permis aux météorologistes de
résoudre leur plus grand problème, à savoir la collecte d’une multitude de données
se rapportant aux échelles synoptiques, sub-synoptique et locale.
I.1. Inventaire des stations nécessaires à l’observation
La terre est divisée en trois types de
zone :
ü
La zone océanique (37.107 km2) ou
les ondes de longueur 3000 à 10000
km à décrire nécessitent un réseau de points dont la
maille est de 600 km.
ü
La zone continentale ( 9. 107 km2)
ou l’orographie détruit les ondes planétaires en ondes plus petites (ondes
synoptiques de 1000 à 3000
km) et dont la distance entre stations ne doit pas excéder
300 km.
ü
La zone continentale à forte densité de population (
5.107 km2) ou pour avoir une bonne prévision, il est
nécessaire de travailler à l’échelle sub-synoptique (distance de maille 150 km au moins).
Tenant
compte de ce qu’on vient d’énoncer, un réseau de 1250 stations d’observations
en altitude est nécessaire pour être dans les normes.
Actuellement
le nombre de stations est très faible surtout aux pays du tiers monde et la
distribution des stations est loin d’être optimale. Le coût de maintenance, les
problèmes de personnel et de télécommunications empêchent ce réseau de croître,
on le voit diminuer quelquefois.
Il
est à noter que l’inventaire ci-dessus se rapporte uniquement aux modèles de
prévisions numériques. Il est entendu que les autres types d’utilisation
requièrent un nombre plus important d’observations dans l’espace et dans le
temps. La surveillance locale du temps nécessite des stations espacées de
quelques dizaines de kilomètres et d’une fréquence d’observation d’une dizaine
de minutes.
I.2. L’avantage des satellites météorologiques
Un
observateur en altitude peut offrir des avantages considérables en face de ce
problème qui est la surveillance globale du temps avec une densité
d’observations qui peut aller jusqu’à la micro échelle.
Une
plate-forme dans une orbite polaire à une altitude de 1500 km ( satellite à
défilement) peut donner une image longue de 40000 km et large de 3000 km toutes les 2 heures
( en ne considérant seulement que la surface convenablement « vue »).
Durant
2 heures la terre tourne de 30° et ainsi la ceinture suivante vue par le
satellite sera contiguë à la première ; donc une seule plate-forme
couvrira le terre en 12 heures, 2 plate-formes en 6 heures et quatre en 3
heures etc…
Si
ces plates-formes sont capables d’effectuer sur leur trajectoire des
radiosondages avec la même précision que les stations, on aura résolu le
problème d’observations.
H : altitude de satellite
: 1500 km
Lv :
bande convenablement vue : 3000
km
Lt : bande vue :
8000 km
satellite
Cependant
des mesures plus fréquentes nécessitent un nombre important de satellites à
défilement ; aussi un satellite géostationnaire (fixe par rapport à la
terre) offre la solution désirée, à savoir la surveillance permanente de la
portion terrestre « vue » par le stellite. Cette portion sous
surveillance est assez large, elle est d’à peu près le 1/3 ou le 1/4 de la
surface terrestre, si on considère seulement la surface « vue »
convenablement. D’un autre coté, une seule plate-forme peut voir seulement une
portion déterminée, il est donc nécessaire de disposer d’au moins 5 satellites
autour de la terre. Toutefois les hautes latitudes (> 50°) ne sont pas
servies par le satellite géostationnaire, elles sont au contraire bien servies
par les satellites à défilement qui passent sur les régions polaires
pratiquement toutes les 2 heures.
II. Principe de la radiométrieII.1. Les lois classiques du rayonnement
Il est
évident que le seul signal terrestre qui peut atteindre le satellite est un
signal électromagnétique. Les propriétés macroscopiques d’un corps terrestre
par rapport à la radiation électromagnétique sont résumées au moyen de trois
coefficients mis en équation :
r(λ,T) + t(λ,T) + ε(λ,T) = 1 (1)
r :
réflexion
t :
transmission
ε : absorption
λ : longueur d’onde de la radiation électromagnétique
T :
la température en degré kelvin
Un
corps qui reçoit une radiation en réfléchit une fraction (r), en transmet une
autre à son environnement (t) et en absorbe le reste (ε).
r,t
et ε sont
respectivement la réflexivité, la transmission et l’absorption (appelée
également émissivité pour des raisons que l’on verra plus loin).
Pour
un corps noir, la distribution de l’énergie est donnée par la loi de Planck.
h=6,6256.
10-34 j.s
c=2,9979243.
108 m.s-1
k=1,38.
10-23 j.°k-1
β(λ,T)
est la puissance radiative émise par une surface unité dans un demi-espace par
unité de longueur d’onde. La puissance émise par unité d’angle solide est donné
par :
La
figure 2 illustre la fonction de Planck pour T=6000 ° K (température de la
surface du soleil) et pour T=300° K (température de la surface terrestre).
Figure. 2 :
Représentation graphique de l’équation de Planck (cas terre – soleil)
La partie de droite de la
fonction de Planck suit plutôt la loi de Rayleigh-Jeans:
(3)
Bien
entendu ces lois ne sont valables que pour un corps noir. Un corps noir est par
définition un corps qui absorbe toute l'énergie qu'on lui fournit.
La
puissance émise par un corps noir à la température T est donnée par la loi de
Stefan Boltzmann:
(4)
C'est
l'intégrale de la fonction de Planck dans le domaine [0,∞] des longueurs
d'onde.
σ
étant la constante de Stefan et qui vaut 5,6698.10-5 CGS.
A 273°K,
W(T)=0,0316 w/cm2 = 0,452 cal/cm2/mn.
La
longueur d'onde ou l'on a le maximum d'émission dépend de la température: c'est
la loi de Wien.
(5)
l=0,2891
cm °K
Il
est à noter que d'après la loi de Planck le maximum d'énergie du soleil a lieu
pour λ=0,5 μ et qu'une grande partie de cette énergie est comprise entre 0,2 μ
et 3 μ.
En
ce qui concerne l'énergie émise par la terre, le maximum d'énergie se situe aux
alentours de 10 μ et la plus grande partie est comprise entre 3 μ et 50 μ.
Les
radiations électromagnétiques solaires sont confinées dans la bande visible,
l'ultraviolet et le proche infrarouge; tandis que les radiations électromagnétiques
terrestres sont dans l'infrarouge intermédiaires et éloigné (voir figure 3)
Figure. 3: Le
spectre électromagnétique
Les
lois de Planck (équation 2) et de Wien (équation 5) s'appliquent uniquement au
corps noir. Pour des corps naturels, la loi d'émission doit être déterminée
pour chaque corps souvent expérimentalement. Cependant tout ce qu'on peut dire
est qu'un ensemble de corps de natures différentes à des températures
différentes, après un certain temps, chaque corps atteint l'équilibre thermique
montrant ainsi que la radiation absorbée est compensée par une radiation émise;
c'est le principe de Kirchhoff.
(6)
Ou
Pi (λ,T) représente l'émission du corps i et εi (λ,T) le
coefficient d'absorption de ce corps.
Si
nous écrivons l'équation 6 pour un corps quelconque et un corps noir on a la
relation:
Cette
dernière équation met en évidence le principe fondamental qui est qu'un corps
peut seulement émettre dans les bandes ou il est apte à absorber: c'est
pourquoi on appelle le terme ε utilisé pour désigner l'absorption:
l'émissivité.
II.2. Principe de la télédétection
Télédétection: en latin detegere = découvrir, en grec télé = distance
Définitions:
Les équations (2), (4) et (5) peuvent être
utilisées pour déterminer la température d'un corps noir en mesurant la
radiation émise par celui-ci.
L'équation
de Stefan Boltzman (4) intègre toutes les longueurs d'onde, nécessite donc un
radiomètre avec réponse sur tout le spectre.
L'équation
de Wien (5) demande un spectromètre pour déterminer la longueur d'onde à
laquelle la radiation est maximale.
L'équation
de Planck (2) nécessite un radiomètre répondant à une longueur d'onde
déterminée à ± Δλ; et donc c'est cette dernière qui est utilisée.
Si
la fonction filtrante du radiomètre est A(λ), le signal enregistré par le
radiomètre à bord du satellite serait:
Le second membre de cette équation devrait être multiplié par ε (l'émissivité) pour tenir compte des corps naturels si ε est connu.
La
fonction filtrante est si étroite que les variations de ε(λ,T) dans
l'intervalle [λ0-Δλ, λ0+Δλ] sont négligeables; la
dépendance de ε avec T est aussi généralement négligeable.
Soit
une source radiative d'intensité Ir, une fraction rIr sera réfléchie en
direction du radiomètre. La terre quant à elle transmet au corps une intensité
It dont une fraction tIt sera transmise au radiomètre par le corps, et il y a
aussi le rayonnement propre du corps εβ. L'intensité totale qui émane du corps
est donc:
I(λ,T)=
ε(λ,T).β (λ,T) + r (λ,T).Ir (λ,T) + t (λ,T).It (λ,T) (9)
Dans la
bande du spectre électromagnétique ou l'atmosphère est transparente (fenêtres
atmosphériques[1]),
l'équation (9) représente le rayonnement qui arrive au radiomètre pour une
mesure de température du corps. La signification exacte va dépendre de la bande
d'onde utilisée et de la fonction filtrante du radiomètre.
Figure. 5

[1] On appelle fenêtre
atmosphérique, la bande de longueur d'onde où l'atmosphère n'absorbe pas de
rayonnement (voir figure.5)
II.2.1 La bande visible
D'après
la fonction de Planck, l'énergie émise par la terre dans le visible est
virtuellement nulle; on ne considère que l'énergie réfléchie.
I(vis) = r(vis).S.sin(α)
(10)
S:
l'intensité du rayonnement solaire
α :
élévation du soleil
La
dépendance avec la température est négligée.
L’imagerie
visible est tributaire de l’incidence des rayons solaires sur les corps et du
pouvoir de réflexion de la surface supérieure de l’objet (nuages, végétation…).
C’est ce qu’on appelle l’albédo.
Les
nuages sont de bons réflecteurs ; par contre, le sol est un mauvais
réflecteur surtout les étendues d’eau.
Le
coefficient de réflectivité d’un nuage dépend de :
•
Son épaisseur
et la dimension de ses particules : plus un nuage est épais et dense plus il réfléchit la
lumière solaire,
•
La nature de
ses particules : un nuage de gouttelettes d’eau apparaît plus brillant
qu’un nuage de glace d’épaisseur comparable,
•
La nature de
sa surface supérieure : une surface supérieure régulière et lisse donne un
aspect plus brillant qu’une surface chaotique.
Albédos caractéristiques
Sur
cette image visible :
Avec
l’imagerie visible on peut distinguer facilement les nuages bas, et avec le
contraste on a une idée sur la forme et l’aspect du nuage. En revanche,
l’imagerie visible présente les limitations suivantes:
•
Détection des nuages fins pratiquement impossible,
•
Difficulté de distinguer la neige et la glace des
nuages,
•
Dépendance par rapport à la géométrie : soleil -
cible – satellite,
•
Images disponibles uniquement en période diurne.
II.2.2 Bandes infrarouges
Dans
l'infrarouge intermédiaire (où nous avons les fenêtres atmosphériques), la
plupart des corps ont une réflexivité voisine de zéro, donc pour la surface
terrestre et nuages épais l'équation (9) se réduit à:
I(λ,T)= ε(λ,T) . β (λ,T) (11)
ε varie très peu avec la température dans ce
domaine de longueur d'ondes.
L’imagerie
en infrarouge (IR) thermique restitue une cartographie de la température de la
surface terrestre et des sommets de nuages. Conventionnellement, l’imagerie IR
est présentée en négatif ; les faibles radiances (Températures
basses) sont représentées en blanc, alors que les fortes radiances
(Températures élevées) sont représentées
en noir. Et entre le blanc et le noir, il y a toute l’échelle du gris
pour différencier la température des objets.

Image infrarouge
METEOSAT8 du 01/02/2006 à 1230TU
Sur
cette image visible :
Avec
l’imagerie visible on peut distinguer facilement les nuages bas, et avec le
contraste on a une idée sur la forme et l’aspect du nuage. En revanche,
l’imagerie visible présente les limitations suivantes:
•
Détection des nuages fins pratiquement impossible,
•
Difficulté de distinguer la neige et la glace des
nuages,
•
Dépendance par rapport à la géométrie : soleil -
cible – satellite,
•
Images disponibles uniquement en période diurne.
II.2.2 Bandes infrarouges
Dans
l'infrarouge intermédiaire (où nous avons les fenêtres atmosphériques), la
plupart des corps ont une réflexivité voisine de zéro, donc pour la surface
terrestre et nuages épais l'équation (9) se réduit à:
I(λ,T)= ε(λ,T) . β (λ,T) (11)
ε varie très peu avec la température dans ce
domaine de longueur d'ondes.
L’imagerie
en infrarouge (IR) thermique restitue une cartographie de la température de la
surface terrestre et des sommets de nuages. Conventionnellement, l’imagerie IR
est présentée en négatif ; les faibles radiances (Températures
basses) sont représentées en blanc, alors que les fortes radiances
(Températures élevées) sont représentées
en noir. Et entre le blanc et le noir, il y a toute l’échelle du gris
pour différencier la température des objets.
La
température a une relation avec l’altitude ; plus la température est basse
plus l’altitude est élevée et vis versa. On peut donc distinguer entre les
différentes couches nuageuses : classement possible par tranche
d’altitude ; les nuages blancs sont situés à des niveaux élevés, alors que
les nuages gris sont à des niveaux bas.
A
titre d’exemple : La partie entourée en rouge (1) sur les deux images
montre des nuages situés à l’étage élevé ; ils apparaissent en blanc sur
l’image infrarouge (une température basse), sur l’image visible ils
apparaissent gris (nuages fins).
La
partie marquée par les rectangles verts (2) sur les deux images représente des
nuages bas ; ils sont gris sur l’image infrarouge (température
relativement chaude) et blancs sur l’image visible (nuages reflétant la
lumière).
Les
variations de températures observées sur l’imagerie infrarouge dépendent de la
latitude et proviennent de l’évolution diurne ou des effets saisonniers. Des
nuages de glace seront d’un même blanc, s’ils ont une température similaire,
alors qu’ils peuvent se situer à 12 000 m et plus dans les régions équatoriales
et à 5000 m
dans les régions polaires.
Les
avantages de l’imagerie infrarouge sont :
•
Image disponible
le jour comme la nuit,
•
Les nuages fins
et transparents (genre Cirrus) sont détectables,
•
Extraction
directe de la température de brillance des nuages,
•
On distingue
facilement le contraste terre – mer.
Par
contre l’imagerie infrarouge présente les limitations suivantes:
•
Nuages bas et
brouillards difficilement détectables,
•
Influence des
variations diurnes et saisonnières.
II.3 L'influence de l'air atmosphérique en télédétection
Nous
avons déjà établi que le rayonnement provenant d'une cible hétérogène (mer,
terre, nuage) est donné par l'équation (9);
I(λ,T)=
ε(λ,T).β (λ,T) + r (λ,T).Ir (λ,T) + t (λ,T).It (λ,T) (9)
Cette
intensité atteint le radiomètre à bord du satellite dans les longueurs d'ondes
correspondant aux fenêtres atmosphériques. Mais si l'atmosphère est absorbante
dans cette bande, il faut considérer le phénomène d'absorption et de rémission
des différentes couches de l'atmosphère.
La
mesure utilisant les bandes d'absorption peut donner des informations sur
l'état de l'atmosphère surtout si on se place dans les bandes spectrales à
fortes absorptions (mesure du profil vertical de température et d'humidité).
Dans
l'infrarouge intermédiaire (où nous avons les fenêtres d'absorption, voir
figure 5), l’imagerie en infrarouge vapeur d’eau restitue une cartographie de
la vapeur d’eau sur des épaisseurs de l’atmosphère : sondage à plusieurs niveaux.
Conventionnellement,
l’imagerie WV est présentée en négatif :
•
air humide
en haute troposphère (Températures basses dominantes) représenté en blanc,
•
air sec
en haute atmosphère (Températures élevées dominantes) représenté en noir.
Le
canal vapeur d’eau révèle :
•
les liaisons
entre les masses nuageuses et les sources de vapeur d’eau,
•
les transports
verticaux de vapeur d’eau.
Sur
l’image WV ci-dessous, on distingue bien la distribution de la vapeur d’eau sur
le niveau de l’atmosphère où le radiomètre a fait le sondage (vers 9000 m; canal 6.2). On
remarque que la partie entourée par l’ellipse rouge est blanche (existence de
vapeur d’eau), tandis que la partie marquée par le rectangle vert est grise
allant vers le noir (absence de vapeur
d’eau à ce niveau, les nuages sont à un niveau plus bas).
III.2. Utilisation synoptique de l'imageIII.2.1. Identification des nuages
Dans l'infrarouge ces nuages sont moins
blancs que les sommets des Cumulonimbus ou Cumulus car ils ont une faible émissivité
(0,3).
Ils sont brillants dans le visible et
gris ou blancs dans l'infrarouge (moins
blancs par rapport aux sommets des
Cumulonimbus).
Les Cu congestus et médiocris ont également
une forme ovale. Ils sont moins
brillants que les Cb dans l'infrarouge.
A noter que les Ac cas qui ont une
extension verticale importante apparaissent
brillants dans l'infrarouge mais on peut
les distinguer des Cb par la forme du
sommet.
Stratus
et brouillards: la discrimination entre ces nuages est pratiquement impossible,
mais ils se distinguent aisément du reste des nuages par la couleur sombre dans
l'infrarouge et blanche dans le visible.
III.2.2. Analyse synoptique des masses nuageuses
Quand on regarde une image
satellite de dimensions importantes, la principale caractéristique est
l'organisation des nuages en systèmes nuageux.
III.2.2.1. systèmes perturbés
On
reconnaît aisément le système dépressionnaire typique avec front froid, front
chaud et occlusion. La surface frontale froide est souvent bien apparente
suivie la plupart du temps d'un grand nombre de nuages de dimensions réduites
(Cumulus) séparés par des interstices de ciel clair (voir figure 6 ci-dessous) qui
constituent la zone de traîne. Quant à la surface frontale chaude, elle est
parfois moins apparente (ce n'est pas le cas sur la figure 6). L'amas nuageux
est plus important au voisinage du point triple.
Vous
remarquez que l'image n'est d'aucune utilité pour la localisation exacte des
fronts au sol à cause des caractères stable ou instable de l'air chaud, de
l'étalement des Cirrus sous le vent et aussi de l'erreur de
"paralaxe" qui s'introduit si le nuage n'est pas situé sur la verticale
du satellite.
III.2.2.2. Les systèmes orageux et la Z.C.I.T
Les systèmes orageux et la Z.C.I.T sont constitués
essentiellement par des Cumulonimbus; les images satellitales montrent des amas
nuageux cirriformes et cumuliformes. La partie active du Cumulonimbus est
caractérisée par des bourgeonnements apparents dans le visible et le contour le
plus froid dans l'infrarouge (voir images ci-dessous). Cette partie active est
très souvent moins étendue que la partie inactive constituée par les Cirrus
denses de l'enclume (forme de carotte).
Dans le système orageux,
un aspect de l'évolution est clair lorsqu'on parcourt une série d'images
consécutives (voir la série d'images ci-dessous de 10h00 à 11h00).
D'une façon générale la
zone intertropicale est caractéristique des nuages cumuliformes. La zone de
convergence intertropicale est mieux organisée sur l'océan, car sur le
continent la convection diurne augmente la masse nuageuse et détruit la notion
relativement étroite qu'on a de la
Z.C.I.T.
Image IR (10.8)
III.2.2.3. le ciel en dehors des systèmes organisés
Quand le ciel n'est pas
clair, les zones de brouillard, de stratus ou de Cumulus de beau temps sont
nettement visibles dans les intervalles secteurs chauds ou zones de liaison:
Ils apparaissent brillants dans le visible et gris sombre (relativement chaud)
dans l'infrarouge.


*SEVIRI :
Le nom du
radiomètre à bord du satellite MSG1(METEOSAT8)
Canal vis (0.6 mm) Canal
vis (0.8 mm)
MSG-1, 24 juin 2003, 15:30 TU
Sur
les deux images ci-dessus, malgré que les deux canaux donnent une identification
des nuages par réflexion du rayonnement solaire ; on constate qu’on a une
meilleure identification des structures de surface en VIS 0,8 qu’en visible
0,6. Cela est du à ce que la réflectance du sol et de la végétation sont plus
importantes dans la longueur d’onde 0,8 mm que dans la longueur d’onde 0,6 mm
(voir figure 7). Le même principe s’applique sur le spectre infrarouge. Quant
au canal vapeur d’eau 7,3 mm, il donne la distribution de la
vapeur d’eau existante dans la couche située entre 700 hpa et 300 hpa (entre 3000 m et 9200 m) ; alors que
celui 6,2 mm, il identifie cette distribution entre 500 hpa et 200
hpa (entre 5600 m
et 11000 m).
Le
tableau suivant indique quelques atouts pour lever quelques ambiguïtés de
détection.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







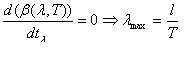













Aucun commentaire:
Enregistrer un commentaire